人工智能中的手段 - 结束分析
- 前面已经学习了向前或向后推理的策略,但是两个方向的混合适合于解决复杂和大的问题。这样一种混合策略,使得有可能首先解决问题的主要部分,然后回过头来解决在组合问题的大部分期间出现的小问题。这种技术称为手段 - 末端分析。
- Means-Ends分析是人工智能中用于限制AI程序中搜索的问题解决技术。
- 它是向后和向前搜索技术的混合体。
- MEA技术于1961年由Allen Newell和Herbert A. Simon首先在他们解决问题的计算机程序中引入,该程序被命名为通用问题解算器(GPS)。
- MEA分析过程的核心是评估当前状态和目标状态之间的差异。
手段结束分析的工作原理
手段-结束分析过程可以递归地应用于问题。这是一种控制解决问题搜索的策略。以下是描述MEA技术解决问题的主要步骤。
首先,评估初始状态和最终状态之间的差异。
- 选择可应用于每个差异的各种运算符。
- 在每个差异处应用运算符,它减少了当前状态和目标状态之间的差异。
运算符子目标
在MEA过程中,检测当前状态和目标状态之间的差异。当出现这些差异,我们就可以应用运算符来减少差异。但有时可能无法将操作员应用于当前状态。因此,我们创建当前状态的子问题,其中可以应用运算符,这种类型的反向链接,其中选择运算符,然后设置子目标以建立运算符的前提条件,称为运算符子目标。
均值分析算法
当将当前状态作为CURRENT和目标状态作为GOAL,然后是MEA算法的步骤。
- 步骤1:将CURRENT与GOAL进行比较,如果两者之间没有差异,则返回Success和Exit。
- 步骤2:否则,选择最显着的差异并通过执行以下步骤来减少它,直到成功或失败发生。
- 选择适用于当前差异的新运算符O,如果没有这样的运算符,则表示信号失败。
- 尝试将运算符O应用于CURRENT。
上面讨论的算法更适合于一个简单的问题,并不足以解决复杂的问题。
均值 - 分析的例子
下面举一个例子,我们知道下面给出的初始状态和目标状态。在这个问题中,需要通过找到初始状态和目标状态之间的差异以及应用运算符来获得目标状态。
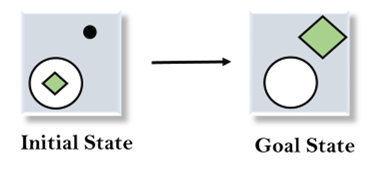
解决:
为了解决上述问题,将首先找到初始状态和目标状态之间的差异,并且对于每个差异,我们将生成一个新状态并将应用运算符。解决这个问题的运算符是:
- 移动
- 删除
- 扩展
1.评估初始状态: 在第一步中,将评估初始状态,并将比较初始状态和目标状态,以找出两个状态之间的差异。

2.应用删除运算符: 可以检查第一个区别是在目标状态中没有出现在初始状态的点符号,因此,首先将应用肉删除运算符来删除此点。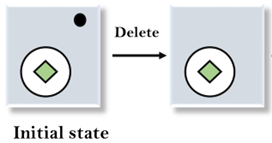
3. 应用移动运算符:应用删除运算符后,将出现新状态,将再次与目标状态进行比较。在比较这些状态之后,另一个区别是方形在圆外,因此将应用移动运算符。
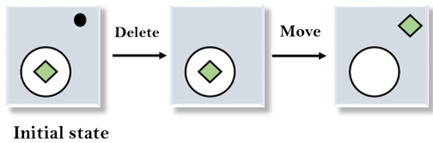
4. 应用Expand运算符:现在在第三步中生成一个新状态,将此状态与目标状态进行比较。在比较状态之后,仍然存在一个差异,即方形的大小,因此,将应用Expand运算符,最后,它将生成目标状态。
