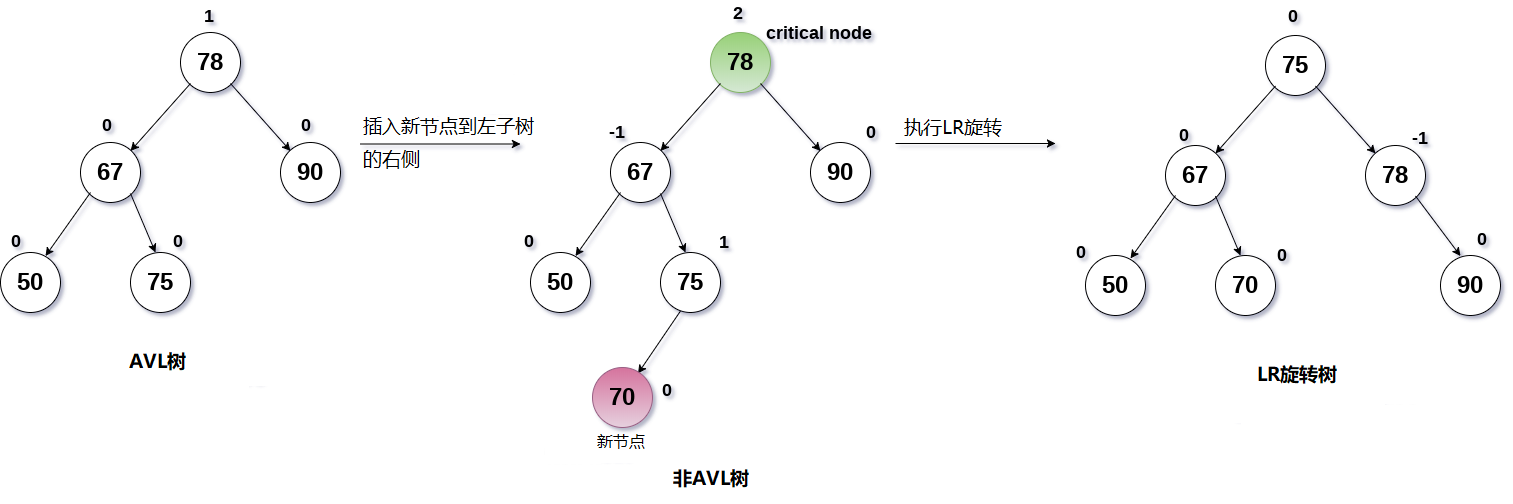
如果将新节点插入节点A的左子树的右侧,则执行LR旋转。
在LR旋转中,节点C(如图所示)成为树的根节点,而节点B和A分别成为其左右子节点。
T1和T2分别成为节点B的左右子树,而T3和T4成为节点A的左右子树。

示例:
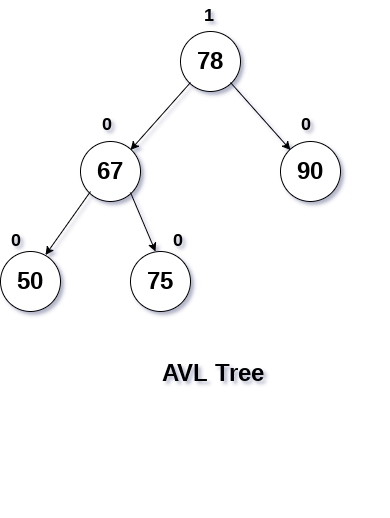
将值为70的节点插入到以下数据结构显示的树中。
解决方案:
根据二叉搜索树的属性,将值为70的节点插入到树根的左子树的右侧。
如图所示,插入70时根节点的平衡因子受到干扰,这成为关键节点A。
要重新平衡树,将执行LR旋转。 节点C即75将成为树的新根节点,其中B和A分别作为其左和右子节点。
子树T1,T2成为B的左右子树,而子树T3,T4成为A的左右子树。
该过程如下图所示。