Prim算法用于从图中查找最小生成树。Prim算法找到包括图的每个顶点的边的子集,使得边的权重之和可以最小化。
Prim算法从单个节点开始,并在每一步探索所有相邻节点的所有连接边缘。 选择了具有最小权重的边缘在图表中没有引起循环。
算法如下 -
第1步:选择一个起始顶点
第2步:重复第3步和第4步,直到有条纹顶点
第3步:选择连接树顶点和具有最小权重的边缘顶点的边`e`。
第4步:将选定的边和顶点添加到最小生成树`T`。
[循环结束]
第5步:退出
示例:
使用prim算法构造下图中给出的图的最小生成树。
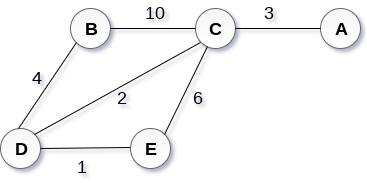
解决方案
第1步:选择一个起始顶点B。
第2步:添加与A相邻的顶点,连接顶点的边用虚线表示。
第3步:选择所有权重最小的边缘,即BD并将其添加到MST。添加D的相邻顶点,即C和E。
第4步:选择所有权重最小的边缘,在这种情况下,边缘DE和CD是这样的边缘。 将它们添加到MST并探索C的相邻,即E和A。
第5步:选择具有最小重量的边缘,即CA。不能选择CE,因为它会导致图中的循环。
在第4步中产生的图形是上图中所示的图形的最小生成树。
MST的成本将按以下方式计算:
成本(MST)= 4 + 2 + 1 + 3 = 10 个单位。

C语言实现示例代码
#include <stdio.h>
#include <limits.h>
#define vertices 5
int minimum_key(int k[], int mst[])
{
int minimum = INT_MAX, min,i;
for (i = 0; i < vertices; i++)
if (mst[i] == 0 && k[i] < minimum )
minimum = k[i], min = i;
return min;
}
void prim(int g[vertices][vertices])
{
int parent[vertices];
int k[vertices];
int mst[vertices];
int i, count,u,v;
for (i = 0; i < vertices; i++)
k[i] = INT_MAX, mst[i] = 0;
k[0] = 0;
parent[0] = -1;
for (count = 0; count < vertices-1; count++)
{
u = minimum_key(k, mst);
mst[u] = 1;
for (v = 0; v < vertices; v++)
if (g[u][v] && mst[v] == 0 && g[u][v] < k[v])
parent[v] = u, k[v] = g[u][v];
}
for (i = 1; i < vertices; i++)
printf("%d %d %d \n", parent[i], i, g[i][parent[i]]);
}
void main()
{
int g[vertices][vertices] = {{3, 2, 1, 9, 0},
{5, 1, 2, 10, 4},
{0, 4, 1, 0, 9},
{8, 10, 0, 2, 10},
{1, 6, 8, 11, 0},
};
prim(g);
}
执行上面示例代码,得到以下结果 -
0 1 5
0 2 0
0 3 8
1 4 6
