MATLAB提供了处理转换的命令,如拉普拉斯和傅里叶变换。转换在科学和工程中被用作简化分析和从另一个角度看待数据的工具。
例如,傅里叶(Fourier)转换允许我们将表示为时间的函数的信号转换为频率的函数。 拉普拉斯变换允许我们将微分方程转换为代数方程。
MATLAB提供了laplace,fourier和fft命令来处理拉普拉斯,傅立叶和快速傅里叶转换。
拉普拉斯变换
时间f(t)函数的拉普拉斯转换由以下积分 -

拉普拉斯变换也表示为f(t)到F(s)的变换。 可以看到此变换或集成过程将f(t),符号变量t的函数转换为另一个函数F(s)与另一个变量s。
拉普拉斯变换将微分方程转换为代数方程。要计算函数f(t)的拉普拉斯变换,参考以下代码 -
laplace(f(t))
示例
在这个例子中,我们将计算一些常用函数的拉普拉斯变换。
创建脚本文件并键入以下代码 -
syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))
MATLAB运行文件代码时,得到以下结果 -
Trial>> syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))
ans =
1/s^2
ans =
2/s^3
ans =
362880/s^10
ans =
1/(b + s)
ans =
w/(s^2 + w^2)
ans =
s/(s^2 + w^2)
逆拉普拉斯变换
MATLAB中可使用命令ilaplace来计算逆拉普拉斯变换。
例如,
ilaplace(1/s^3)
MATLAB执行上述代码语句得到以下结果 -
ans =
t^2/2
示例
创建脚本文件并键入以下代码 -
syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))
MATLAB执行上述代码语句得到以下结果 -
ans =
t^6/720
ans =
2*exp(-t*w)
ans =
cos(2*t)
ans =
ilaplace(exp(-b*t), t, x)
ans =
sin(t*w)
ans =
cos(t*w)
傅里叶变换
傅里叶变换通常将时间f(t)的数学函数转换成有时由F表示的新函数,其参数是以周期/ s(赫兹)或每秒弧度为单位的频率。新功能被称为傅立叶变换和/或函数f的频谱。
示例
创建脚本文件并在其中键入以下代码 -
syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transform
MATLAB执行上述代码语句得到以下结果 -
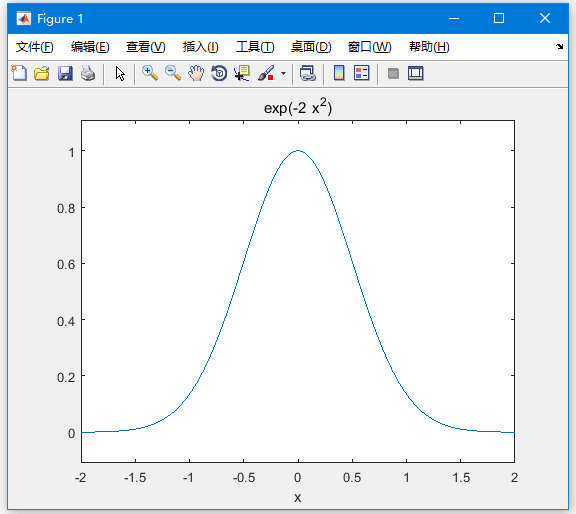
同时也会输出以下结果 -
Trial>> syms x
f = exp(-2*x^2); %our function
ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transform
FT =
(2^(1/2)*pi^(1/2)*exp(-w^2/8))/2
绘制傅里叶变换为 -
syms x
f = exp(-2*x^2); %our function
% ezplot(f,[-2,2]) % plot of our function
FT = fourier(f) % Fourier transform
ezplot(FT)
MATLAB执行上述代码语句得到以下结果 -

逆傅里叶变换
MATLAB提供了用于计算函数的逆傅里叶变换的ifourier命令。 例如,
f = ifourier(-2*exp(-abs(w)))
MATLAB将执行上述语句并显示结果 -
f =
-2/(pi*(x^2 + 1))
